Simular fluidos es el arte de domar la ecuación que los gobierna que no es otra que la ecuación de Navier-Stokes:

$$ \frac{\partial u}{\partial t} = -(u \cdot \nabla) u -\frac{1}{\rho}\nabla P + \upsilon \nabla ^ 2 u  + \frac{1}{\rho} F_{ext} $$

$$\nabla \cdot u = 0$$

Esta ecuación diferencial está catalogada como uno de los problemas del milenio en matemáticas. No se conoce una solución analítica general, salvo en casos muy limitados y concretos.

De hecho, saber siquiera si tiene solución para determinados inputs es, precisamente, el problema del milenio valorado en un millón de dolares.

La forma de lidiar con semejante monstruo es aproximarlo numéricamente.

La simulación

En nuestro caso vamos a simular un fluido en un espacio 2D usando UE4.

El objetivo es el siguiente:

1. Utilizar la ecuación Navier-Stokes para calcular en cada instante y para cada posición 2D la velocidad del fluido. De hecho lo haremos paso a paso tomando la simulación del frame anterior para calcular la simulación del frame actual.
2. Usar dicha velocidad para simular la evolución de cierta cantidad: por ejemplo un colorante o tinta.
3. Usar la simulación anterior y renderizarla por pantalla.

El instrumento matemático que mapea unas coordenadas del espacio a un vector:

FVector GetVector(const FVector& Coord) const;

Se le denomina campo vectorial.

En post previos usamos texturas para almacenar campos vectoriales. El color $(R, G, B)$ de una coordenada $(x, y)$ de la textura codificaba la velocidad en dicho punto.

Aquí también usaremos texturas para almacenar campos vectoriales. En concreto, la velocidad del fluido en un frame.

Análogamente también existen campos escalares.

float GetVector(const FVector& Coord) const;

Antes de entrar en materia vamos a familiarizarnos con la ecuación Navier-Stokes.

Nota importante: Para seguir las matemáticas que se presentan en este artículo hay que tener conocimientos muy básicos de cálculo vectorial: qué es un gradiente y un divergente, principalmente. No necesitas saber calcularlos analíticamente ni usaremoso ningún teorema o resultado acerca de ellos.

Nota 2: Si prefieres pasar de las matemáticas e ir directamente a los materiales en UE4 haciendo un acto de fé lo tienes al final del post.

Deducción de la ecuación Navier-Stokes

Partiendo de la segunda ley de Newton para cuerpos discretos:

$$ F = m a = \frac{d}{dt}(mv) $$

Vamos a intentar adaptarla para cuerpos contínuos, esto es, gases y fluidos en general.

Primeramente, en cuerpos contínuos tiene más sentido hablar de la densidad $\rho$ que la masa como un todo:

$$ F = \frac{d}{dt}(\rho v) $$

Si asumimos que el líquido (o gas) no puede ser comprimido (incompresible), por ejemplo el agua, entonces la densidad es constante con respecto al tiempo:

$$ F = \rho \frac{dv}{dt} $$

Esto obviamente no tiene por qué ser así. Por ejemplo el aire sí es comprimible y por tanto para el aire la suposición anterior sería inválida.

Nuestra simulación es para fluidos incompresible así que daremos la suposición como cierta.

Dado que $v$ en fluidos normalmente se refiere a viscosidad, vamos a renombrar la velocidad de un fluido de $v$ a $u$ para evitar confusiones:

$$ F = \rho \frac{du}{dt} $$

Empecemos por la parte derecha de la ecuación.

¿Qué podemos decir del cambio de velocidad de un fluido?

La velocidad de un fluido varía en cada punto e instante, o dicho de otro modo, la velocidad está en función del espacio y tiempo:

$$ \frac{du}{dt} = \frac{d}{dt} u(p, t) = \frac{\partial u}{\partial t}\frac{dt}{dt} + \frac{\partial u}{\partial x}\frac{dx}{dt} + \frac{\partial u}{\partial y}\frac{dy}{dt} + \frac{\partial u}{\partial z}\frac{dz}{dt}$$

Usando el operador $\nabla$ (nabla) podemos reescribir la ecuación anterior del siguiente modo:

$$ \frac{du}{dt} = \frac{d}{dt} u(x, t) = \frac{\partial u}{\partial t} + (u \cdot \nabla) u $$

Las expresiones de la forma $(v \cdot \nabla) v$ se llaman derivadas direccionales. La derivada $dx/dt$ indica el cambio de $x$ con respecto a $t$ en la base canónica. Una derivada direccional indica igualmente el cambio pero "moviéndonos" en dirección $v$.

Sustitutendo en la ecuación anterior de Newton nos queda:

$$ F = \rho \frac{\partial u}{\partial t} + \rho (u \cdot \nabla) u $$

Tratada la parte derecha, vamos ahora con la parte izquierda de la ecuación. ¿Qué podemos decir en cuanto a las fuerzas de un fluido?

Podemos descomponer la fuerza $F$ en tres componentes; una fuerza exterior (por ejemplo la gravedad, chocar contra una pared, etc.,) y dos "internas" propia de la misma dinámica del fluido consigo mismo:

• La fuerza $F_{visc}$ correspondiente a la viscosidad del fluido, esto es, la fricción interna entre las partículas del fluido.
• La fuerza $F_{p}$ correspondiente al cambio de presión, esto es, el fluido (piensa en un gas) tiende a ocupar los espacios de menor presión.

$$ F = F_{total} = F_{ext} + F_{visc} + F_{p} $$

Sobre la fuerza correspondiente al cambio de presión, hemos dicho que es responsable de que el fluido ocupe zonas de baja presión.

Sea $P$ el campo escalar indicando la presión en cada punto del espacio, podemos calcular el gradiente de $P$ (que se expresa matemáticamente $\nabla P$) que indica la dirección a la que movernos para encontrar zonas de mayor presión.

Por tanto, el fluido se "moverá" justo en dirección contraria al gradiente. Podemos expresar la fuerza $F_{p}$ así:

$$ F_{p} = - \nabla P $$

Es decir, el fluido se "moverá" siguiendo la dirección del gradiente de la presión pero en sentido a zonas de menor presión.

En cuanto a la viscosidad, podemos usar la ley de Newton de la viscosidad que dice, basicamente, que la fuerza es proporcional al gradiente de la velocidad modulado por una constante $\upsilon$ llamada viscosidad kinemática:

$$ F_{visc} = \rho \upsilon \nabla ^ 2 u $$

Poniendo todo junto, obtenemos:

$$ F_{ext} + \rho \upsilon \nabla ^ 2 u  - \nabla P = \rho (\frac{\partial u}{\partial t} + (u \cdot \nabla) u) $$

Reordenando:

$$ \frac{\partial u}{\partial t} = -(u \cdot \nabla) u -\frac{1}{\rho}\nabla P + \upsilon \nabla ^ 2 u  + \frac{1}{\rho} F_{ext} $$

Por último, ¿recuerdas la hipótesis de que el fluido era incompresible?

Un fluido es incompresible si la densidad es constante. Si la densidad cambiase, significaría que se está comprimiendo/descomprimiendo en alguna región.

Que la densidad sea constante es solo posible si la cantidad de flujo que entra en una region es igual a la que sale. En caso contrario la densidad no permanecería constante.

O dicho de otro modo, la divergencia debe ser $0$ para todo el campo de velocidades:

$$\nabla \cdot u = 0$$

Tomando las dos ecuaciones anteriores:

$$ \frac{\partial u}{\partial t} = -(u \cdot \nabla) u -\frac{1}{\rho}\nabla P + \upsilon \nabla ^ 2 u  + \frac{1}{\rho} F_{ext} $$

$$\nabla \cdot u = 0$$

Estas son las ecuaciones Navier-Stokes para fluidos incompresibles.

Tratar Navier-Stokes computacionalmente

La simulación se hace sobre un campo. Hemos hablado de campos escalares, por ejemplo de densidad o presión, y también campos vectoriales, en concreto el de la velocidad.

Un campo (escalar o vectorial) representa una variable contínua sobre un espacio que tiene detalle infinito (ya que se define en incrementos infinitesimales).

¿Cómo representamos un campo computacionalmente?

La opción más simple es usando un grid. Cuanto menor espacio entre celdas, más cerca estaremos del infinitesimal matemático.

De hecho, nosotros usaremos una textura como grid.

Existen otras opciones de presentación como hierarchical grids, irregular meshes, adaptative meshes, particle-based y otras. Cada una con sus ventajas e inconvenientes.

¿Cómo aproximamos los cálculos de derivadas y derivadas parciales? Para aproximarlas numéricamente, usaremos las diferencias finitas.

Básicamente se trata de "relajar" la restricción infinitesimal por una diferencia muy pequeña, pero finita:

$$ \frac{\partial v_i}{\partial x} \approx \frac{v_{i+1} - v_{i-1}}{x_{i+1} - x_{i-1}} = \frac{v_{i+1} - v_{i-1}}{2 \Delta x}$$

Dónde $v_{i+1}, v_{i-1}$ son los vecinos en el grid de $v_i$ en el eje $x$ (en este ejemplo la derivada es con respecto a $x$).

Podemos decir lo mismo de la segunda derivada:

$$ \frac{\partial ^2 v_i}{\partial x ^ 2} \approx \frac{v_{i+1} - 2 v_i + v_{i-1}}{\Delta x ^ 2} $$

Cuando entremos en los detalles concretos de la implementación, necesitaremos un método que dada una coordenada $uv$ en la textura (que codificara un campo escalar/vectorial) nos devuelva los "vecinos". Los píxeles más cercanos.

Algoritmo para resolver Navier-Stokes

Dada la ecuación de Navier-Stokes:

$$ \frac{\partial u}{\partial t} = -(u \cdot \nabla) u -\frac{1}{\rho}\nabla P + \upsilon \nabla ^ 2 u  + \frac{1}{\rho} F_{ext} $$

$$ \nabla \cdot u = 0 $$

Para ilustrar el algoritmo vamos a simplificarlo. Digamos densidad $\rho = 1$ y no intervienen fuerzas exteriores $F_{ext} = 0$.

$$ \frac{\partial u}{\partial t} = \upsilon \nabla ^ 2 u -(u \cdot \nabla) u -\nabla P $$

Así que la evolución del sistema puede ser determinada computacionalmente así:

$$ u_{t+1} = u_t + \Delta t (\upsilon \nabla ^ 2 u_t -(u_t \cdot \nabla) u_t -\nabla P) $$

Del apartado anterior sabemos como aproximar las derivadas de primer y segundo orden. La viscosidad kinemática $\upsilon$ es un parámetro dado al igual que $\Delta t$ y, obviamente, también conocemos los valores de $u$.

Sin embargo, no conocemos $\nabla P$.

¿Cómo procedemos? Vamos a ignorarlo a ver que pasa:

$$ u_{t+1} ^ * = u_t + \Delta t (\upsilon \nabla ^ 2 u_t - (u_t \cdot \nabla) u_t) $$

Fíjate como en este caso conocemos todas las variables, sabemos calcular (aproximar) derivadas y segundas derivadas, y también sabemos representar un campo vectorial $u$. Por lo que sabemos calcular $ u_{t+1}^* $.

Sin embargo, al ignorar el término $\nabla P$ hemos pagado un precio.

En primer lugar obviamente $ u_{t+1}^* \ne u_{t+1} $, y no sabemos hasta que punto son aproximados, quizás no lo sean en absoluto y por tanto no podamos ignorar tan alegremente $\nabla P$.

Y el segundo es que no podemos garantizar la segunda ecuación de Navier-Stokes:

$$ \nabla \cdot u_{t+1}^* = 0 $$

Recuerda que esta ecuación nos indica que el sistema no es divergente, en otras palabras, la densidad permanece constante.

Pero precisamente esta ecuación nos da una pista de lo que debe ocurrir. Si añadimos el término que hemos obviado la ecuación debe cumplirse:

$$ \nabla \cdot (u_{t+1}^* - \Delta t \nabla P) = 0 $$

Reordenando:

$$ \nabla ^ 2 P = \frac{1}{\Delta t} \nabla P \cdot u_{t+1}^* $$

que se trata de la archiconocida (para algunos) Poisson equation que aparece en multitud de campos de la física.

La buena noticia es que hay multitud de métodos numéricos para resolver la ecuación anterior y, por tanto, obtener $\nabla P$.

El algoritmo nos quedaría:

1. Obtener $u_{t+1}^* = u_t + \Delta t (\upsilon \nabla ^ 2 u_t -(u_t \cdot \nabla) u_t)$
2. Resolver la ecuación Poisson: $ \nabla ^ 2 P = \frac{1}{\Delta t} \nabla P \cdot u_{t+1}^* $
3. Conseguir finalmente $u_{t+1} = u_{t+1} ^ * - \Delta t \nabla P$

Resolver la ecuación Poisson es la clave. Es el paso fundamental para la simulación de fluidos.

Tenemos varios métodos para resolver la ecuación Poisson, probablemente el más sencillo sea usando Jacobi.

No vamos a entrar a discutir en profundidad los métodos matemáticos y no es necesario conocer los detalles. Pero si sientes curiosidad, el siguiente enlace detalla el método.

Preparación del proyecto

Crea una nueva clase Pawn en mi caso la he llamado FluidSimPawn.

Vamos a representar los campos vectoriales/escalares con una textura. En anteriores tutoriales creamos Render Target desde el propio Content Browser. En este ocasión, dado que serán varias texturas, vamos a crearlas dinámicamente por código.

La primera iteración de la clase FluidSimPawn es como sigue:

UCLASS()
class FLUIDSIM_API AFluidSimPawn : public APawn
{
    GENERATED_BODY()

public:
    // Sets default values for this pawn's properties
    AFluidSimPawn();

    // Settings

    UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
    float GridSize;
    
    UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
    float BrushSize;

    // Components

    UPROPERTY(VisibleAnywhere, BlueprintReadOnly, Category = "FluidSim")
    class UCameraComponent* CameraComponent;

    // Render Targets
    // ...

    // Shaders
    // ...

public:

    UPROPERTY(VisibleInstanceOnly, BlueprintReadOnly, Category = "FluidSim")
    bool bIsPainting;

    UPROPERTY(VisibleInstanceOnly, BlueprintReadOnly, Category = "FluidSim")
    FVector2D LastPos;

protected:
    // Called when the game starts or when spawned
    virtual void BeginPlay() override;

public:    
    // Called every frame
    virtual void Tick(float DeltaTime) override;

    // Called to bind functionality to input
    virtual void SetupPlayerInputComponent(class UInputComponent* PlayerInputComponent) override;

    bool FindUVCollision(FVector2D& OutUV) const;

    UFUNCTION()
    void BeginPaint();

    UFUNCTION()
    void EndPaint();

    UFUNCTION()
    void MovePaint();

    UFUNCTION()
    void ChangeBrushSize(float Val);

private:

    class UTextureRenderTarget2D* CreateRenderTarget2D();
};

#include "FluidSimPawn.h"

// Sets default values
AFluidSimPawn::AFluidSimPawn()
{
     // Set this pawn to call Tick() every frame.  You can turn this off to improve performance if you don't need it.
    PrimaryActorTick.bCanEverTick = true;

    GridSize = 256.0f;

    RootComponent = CreateDefaultSubobject<USceneComponent>(TEXT("RootComponent"));
    SetRootComponent(RootComponent);

    CameraComponent = CreateDefaultSubobject<UCameraComponent>(TEXT("CameraComponent"));
    CameraComponent->SetProjectionMode(ECameraProjectionMode::Orthographic);
    CameraComponent->SetOrthoWidth(720.0f);
    CameraComponent->SetupAttachment(RootComponent);

    AutoPossessPlayer = EAutoReceiveInput::Player0;
}

// Called when the game starts or when spawned
void AFluidSimPawn::BeginPlay()
{
    Super::BeginPlay();

    APlayerController* PC = Cast<APlayerController>(GetController());
    PC->bShowMouseCursor = true;    
}

// Called every frame
void AFluidSimPawn::Tick(float DeltaTime)
{
    Super::Tick(DeltaTime);

    if (bIsPainting)
    {
        MovePaint();
    }    

}

// Called to bind functionality to input
void AFluidSimPawn::SetupPlayerInputComponent(UInputComponent* PlayerInputComponent)
{
    Super::SetupPlayerInputComponent(PlayerInputComponent);

    PlayerInputComponent->BindAction(FName(TEXT("Paint")), IE_Pressed, this, &AFluidSimPawn::BeginPaint);
    PlayerInputComponent->BindAction(FName(TEXT("Paint")), IE_Released, this, &AFluidSimPawn::EndPaint);

    PlayerInputComponent->BindAxis(FName(TEXT("BrushSize")), this, &AFluidSimPawn::ChangeBrushSize);
}

bool AFluidSimPawn::FindUVCollision(FVector2D& OutUV) const
{
    APlayerController* PC = Cast<APlayerController>(GetController());

    FVector2D MouseScreenPos;
    PC->GetMousePosition(MouseScreenPos.X, MouseScreenPos.Y);

    FVector MouseWorldPos, MouseWorldDir;
    UGameplayStatics::DeprojectScreenToWorld(PC, MouseScreenPos, MouseWorldPos, MouseWorldDir);

    FCollisionQueryParams QueryParams;
    QueryParams.AddIgnoredActor(this);
    QueryParams.bReturnFaceIndex = true;
    QueryParams.bTraceComplex = true;

    FHitResult Hit;
    bool bHit = GetWorld()->LineTraceSingleByChannel(Hit, MouseWorldPos, MouseWorldPos + 100000.0f * MouseWorldDir, ECC_Visibility, QueryParams);
    if (bHit)
    {
        return UGameplayStatics::FindCollisionUV(Hit, 0, OutUV);
    }

    return false;
}

void AFluidSimPawn::BeginPaint()
{
    bIsPainting = true;
    FindUVCollision(LastPos);
}

void AFluidSimPawn::EndPaint()
{
    bIsPainting = false;
}

void AFluidSimPawn::MovePaint()
{
    if (!bIsPainting)
    {
        return;
    }

    FVector2D CurrentPos;
    FindUVCollision(CurrentPos);
    
    FVector2D FluidVel = CurrentPos - LastPos;
    if (FMath::IsNearlyZero(FluidVel.Size()))
    {
        return;
    }
    
    // ESCRIBIR VELOCIDAD

    LastPos = CurrentPos;
}

void AFluidSimPawn::ChangeBrushSize(float Val)
{
    BrushSize += 0.01 * Val;
}

UTextureRenderTarget2D* AFluidSimPawn::CreateRenderTarget2D()
{    
    UTextureRenderTarget2D* RT = UKismetRenderingLibrary::CreateRenderTarget2D(this, GridSize, GridSize, RTF_RGBA16f);    
    if (RT == NULL)
    {
        UE_LOG(LogTemp, Error, TEXT("CreateRenderTarget2D failed (NULL)"));
        return NULL;
    }

    RT->AddressX = TextureAddress::TA_Clamp;
    RT->AddressY = TextureAddress::TA_Clamp;
    RT->MipsSamplerFilter = TextureFilter::TF_Bilinear;
    
    return RT;
}

El código anterior está explicado en el tutorial sobre Render Target.

Crear los campos vectoriales/escalares

Del algoritmo esbozado de Navier-Stokes necesitamos los siguientes campos:

• Dye (Colorante). En nuestro caso vamos a simular un colorante, como una especie de tinta. Necesitamos un campo escalar indicando en cada punto la cantidad y color del colorante.
• Velocity. El más importante, el objetivo principal, es el que debemos calcular y mantener actualizado. El resto de campos se usan como cálculos intermedios para éste. Usaremos el campo velocidad para actualizar el Colorante.
• Pressure. El campo que resolveremos usando Jacobi.
• Divergence. Campo intermedio dónde almacenaremos los cálculos del operador divergencia de la velocidad.

Conceptualmente estos son los campos/texturas que necesitamos. Técnicamente necesitamos algunas texturas más, ¿por qué?

Basicamente cuando actualicemos (escribir) la textura velocidad también necesitamos "leer" de la misma textura velocidad. No podemos escribir/leer a la vez una misma textura, cosas malas ocurrirían.

En vez de eso, usaremos texturas secundarias dónde copiaremos las texturas "primarias" con objeto de poder leer mientras escribimos.

Añade las siguientes texturas:

// Render Targets

UPROPERTY(VisibleAnywhere, BlueprintReadOnly, Category = "FluidSim")
class UTextureRenderTarget2D* VelocityField;

UPROPERTY(VisibleAnywhere, BlueprintReadOnly, Category = "FluidSim")
class UTextureRenderTarget2D* VelocityFieldRead;

UPROPERTY(VisibleAnywhere, BlueprintReadOnly, Category = "FluidSim")
class UTextureRenderTarget2D* DyeField;

UPROPERTY(VisibleAnywhere, BlueprintReadOnly, Category = "FluidSim")
class UTextureRenderTarget2D* DyeFieldRead;

UPROPERTY(VisibleAnywhere, BlueprintReadOnly, Category = "FluidSim")
class UTextureRenderTarget2D* PressureField;

UPROPERTY(VisibleAnywhere, BlueprintReadOnly, Category = "FluidSim")
class UTextureRenderTarget2D* PressureFieldRead;

UPROPERTY(VisibleAnywhere, BlueprintReadOnly, Category = "FluidSim")
class UTextureRenderTarget2D* DivergenceField;

E instancialas en BeginPlay:

void AFluidSimPawn::BeginPlay()
{
    Super::BeginPlay();

    VelocityField = CreateRenderTarget2D();
    VelocityFieldRead = CreateRenderTarget2D();
    DyeField = CreateRenderTarget2D();
    DyeFieldRead = CreateRenderTarget2D();
    PressureField = CreateRenderTarget2D();
    PressureFieldRead = CreateRenderTarget2D();
    DivergenceField = CreateRenderTarget2D();

    APlayerController* PC = Cast<APlayerController>(GetController());
    PC->bShowMouseCursor = true;    
}

Como hemos dicho, necesitaremos copiar los contenidos de las texturas primarias (por ejemplo, PressureField) a las secundarias (PressureFieldRead).

Crea un material para copiar una textura:

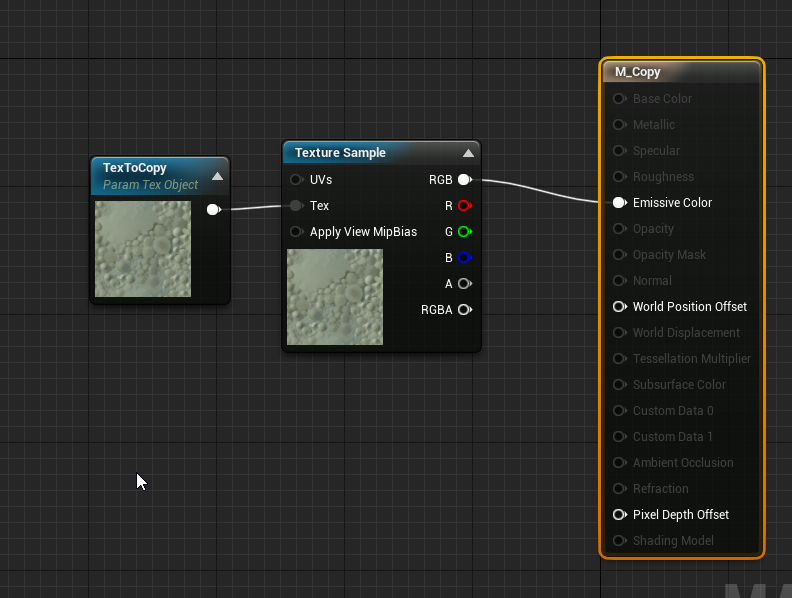
Añade propiedades para referenciarlo:

public:
UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
UMaterialInterface* CopyShaderBase;

private:
UPROPERTY()
class UMaterialInstanceDynamic* CopyShader;	

Y en BeginPlay:

void AFluidSimPawn::BeginPlay() {
    // ...
    CopyShader = UMaterialInstanceDynamic::Create(CopyShaderBase, this);
}

Por último, vamos a implementar un método que haga uso de este material:

protected:
void FluidCopy(class UTextureRenderTarget2D* CopyTo, class UTexture* CopyFrom);

void AFluidSimPawn::FluidCopy(UTextureRenderTarget2D* CopyTo, UTexture* CopyFrom)
{
    CopyShader->SetTextureParameterValue(FName(TEXT("TexToCopy")), CopyFrom);
    UKismetRenderingLibrary::DrawMaterialToRenderTarget(this, CopyTo, CopyShader);
}

Como puedes ver en el código, hacemos uso de DrawMaterialToRenderTarget para renderizar todo el material sobre la textura.

Vamos a completar la parte marcada por el comentario:

// ESCRIBIR VELOCIDAD

Podríamos pintar, como hemos hecho en tutoriales anteriores, usando los métodos:

UKismetRenderingLibrary::BeginDrawCanvasToRenderTarget(this, RenderTarget, Canvas, Size, Context);

// ...
Canvas->K2_DrawMaterial(BrushMaterial, ScreenPos, ScreenSize, FVector2D::ZeroVector);
// ...
	
UKismetRenderingLibrary::EndDrawCanvasToRenderTarget(this, Context);

Y sería completamente válido. Sin embargo, vamos a usar una aproximación diferente.

En esta ocasión vamos a seguir usando el método:

UKismetRenderingLibrary::DrawMaterialToRenderTarget(this, TextureTarget, AnyMaterial);

Que "pinta" todo el material en la textura.

Por tanto, el material que estamos buscando necesita tomar como entradas:

• Una textura base
• Unas coordenadas UV dónde pintar un color
• El color que vamos a pintar
• El radio del pincel

El material tendría la siguiente pinta:

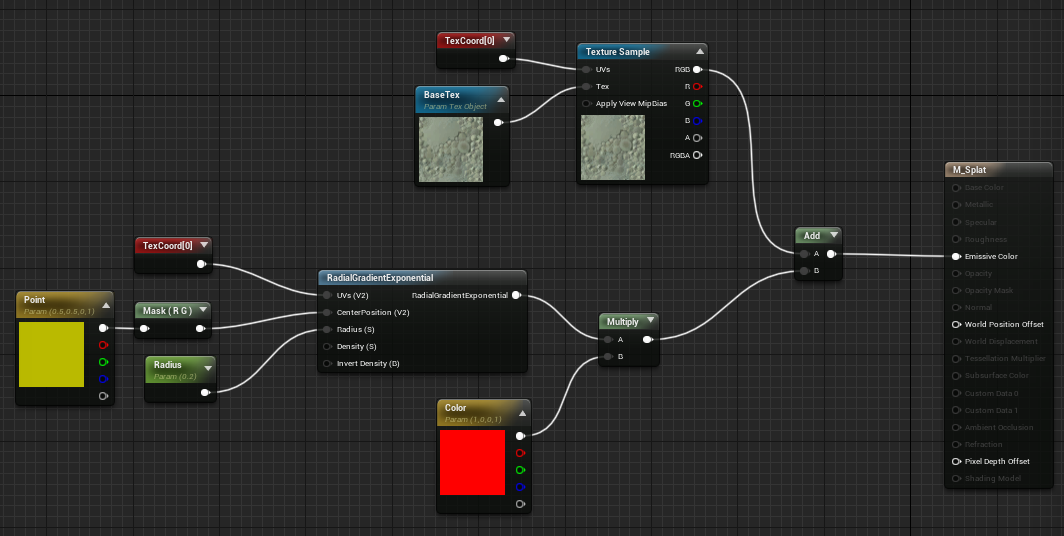
Vamos a añadir el método:

void FluidSplat(class UTextureRenderTarget2D* Splatted, FVector2D& Coord, const FLinearColor& Color, float Radius, class UTexture* BaseTex);

Cuya implementación:

void AFluidSimPawn::FluidSplat(UTextureRenderTarget2D* Splatted, FVector2D& Coord, const FLinearColor& Color, float Radius, UTexture* BaseTex)
{
	SplatShader->SetTextureParameterValue(FName(TEXT("BaseTex")), BaseTex);
	SplatShader->SetVectorParameterValue(FName(TEXT("Point")), FLinearColor(Coord.X, Coord.Y, 0.0f, 0.0f));
	SplatShader->SetVectorParameterValue(FName(TEXT("Color")), Color);
	SplatShader->SetScalarParameterValue(FName(TEXT("Radius")), Radius);
	UKismetRenderingLibrary::DrawMaterialToRenderTarget(this, Splatted, SplatShader);
}

Al igual que con copy necesitamos añadir una referencia del material a la clase:

public:
UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
UMaterialInterface* SplatShaderBase;

private:
UPROPERTY()
class UMaterialInstanceDynamic* SplatShader;

void AFluidSimPawn::BeginPlay()
{
    // ...	
    SplatShader = UMaterialInstanceDynamic::Create(SplatShaderBase, this);
    // ...
}

Ahora ya podemos completar el código del método Paint:

void AFluidSimPawn::MovePaint()
{
    if (!bIsPainting)
    {
        return;
    }

    FVector2D CurrentPos;
    FindUVCollision(CurrentPos);
    
    FVector2D FluidVel = CurrentPos - LastPos;
    if (FMath::IsNearlyZero(FluidVel.Size()))
    {
        return;
    }
    
    // Pintar velocidad
    
    FLinearColor VelocityColor = FLinearColor(SplatForce * FluidVel.X, SplatForce * FluidVel.Y, 0.0f, 1.0f);
 
    FluidCopy(VelocityFieldRead, VelocityField);
    FluidSplat(VelocityField, LastPos, VelocityColor, BrushSize, VelocityFieldRead);

    // Pintar algo de colorante

    const FLinearColor DyeColor = FLinearColor(1.0f, 0.0f, 0.0f, 1.0f);
    
    FluidCopy(DyeFieldRead, DyeField);    
    FluidSplat(DyeField, LastPos, DyeColor, BrushSize, DyeFieldRead);

    LastPos = CurrentPos;
}

Dónde SplatForce es un atributo que funciona a modo de multiplicador. Puedes jugar con él asignándole distintos valores:

UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
float SplatForce; // por defecto 5000 funciona bien

Un aspecto de crucial importancia. Fíjate como codificamos la velocidad en un color. Potencialmente estamos pasando valores negativos como color a una textura.

Podrías proceder tal y como hicimos en el tutorial de flowmaps y codificar/decodificar la velocidad en un color válido. Sin embargo, UE4 trae una solución más sencilla si no nos importa que existan colores negativos.

Para que un material pueda escribir colores negativos, debes marcarlo en el editor de materiales:

Para este tutorial, marca Allow Negative Emissive Color en todos los materiales que crees, incluidos los dos materiales que llevamos por ahora: M_Copy y M_Splat.

Si todo va bien deberías poder pintar tanto la velocidad como el colorante en sus respectivas texturas:

Pues sin querer queriendo ya hemos desarrollado la parte de la ecuación de Navier-Stokes referente a las fuerzas externas, ¡hemos pintado la velocidad!

Implementación del algoritmo

Vamos a implementar el algoritmo que describimos previamente.

Necesitaremos algunos métodos para cálculos intermedios.

Uno de ellos será computar la divergencia de un campo. En concreto del campo de velocidad.

También necesitaremos computar el gradiente.

Ambos cálculos serán implementados usando el método de diferencias finitas.

Para usar diferencias finitas, tal y como vimos, necesitamos acceder a los valores "vecinos".

Implementa el siguiente material function que nos servirá de ayuda:

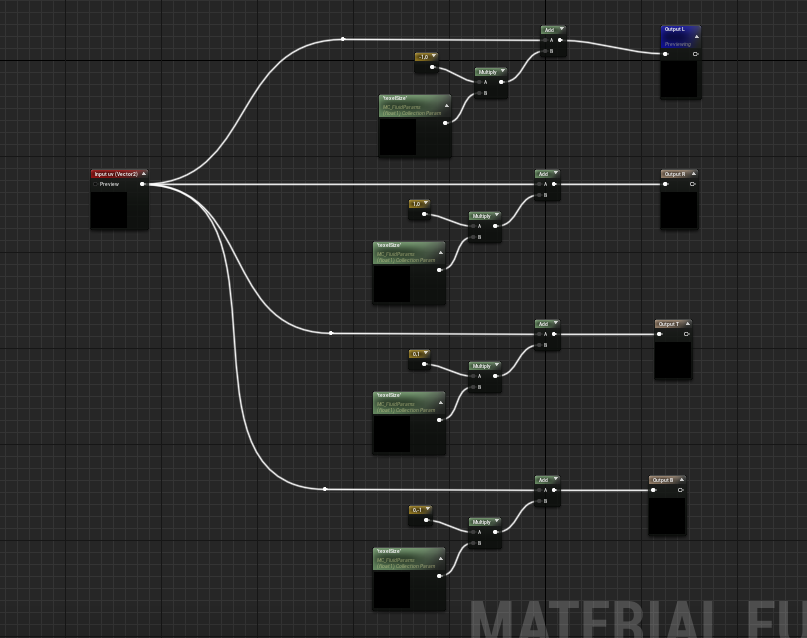
Necesitamos un Material Parameter Collection dónde almacenaremos texelSize. Crea uno, llámalo MC_FluidParams.

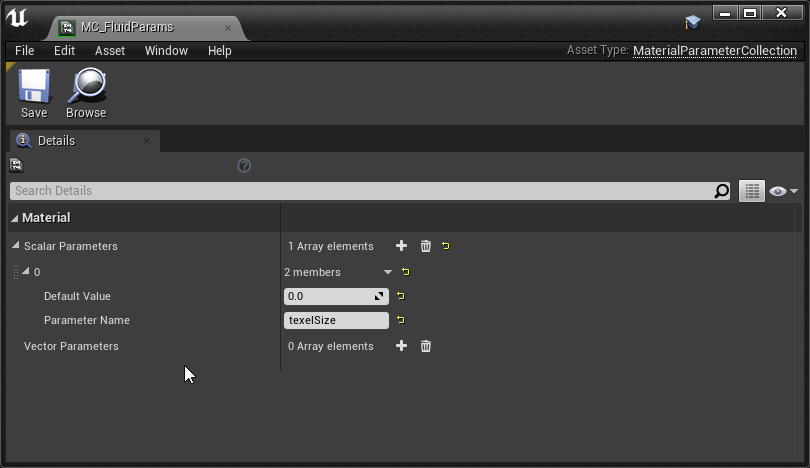
Añade una referencia a la clase Pawn:

public:
UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
class UMaterialParameterCollection* ShaderParams;

E inicializa texelSize en BeginPlay:

void AFluidSimPawn::BeginPlay()
{
    // ...
    UKismetMaterialLibrary::SetScalarParameterValue(this, ShaderParams, FName(TEXT("texelSize")), 1.0f / GridSize);
}

Preparativos listos, vamos con la implementación.

Divergente

Necesitaremos calcular la divergencia del campo de velocidades.

El siguiente material, usando diferencias finitas, la calcula:

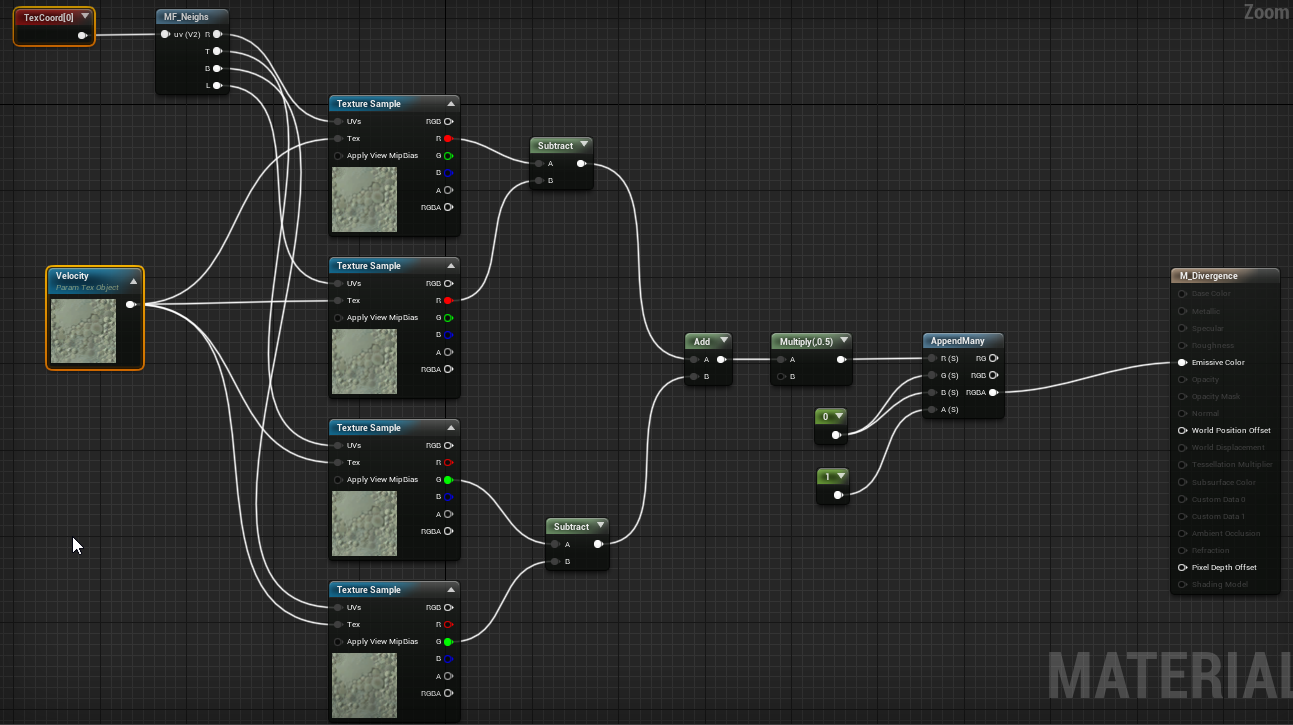
No olvides marcar Allow Negative Emissive Color.

Añade los siguientes métodos y propiedades a la clase Pawn tal y como hemos hecho con materiales previos:

public:
UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
UMaterialInterface* DivergenceShaderBase;

protected:
void FluidDivergence(class UTextureRenderTarget2D* OutDivergence, class UTexture* InVelocity);

private:
UPROPERTY()
class UMaterialInstanceDynamic* DivergenceShader;

void AFluidSimPawn::BeginPlay()
{
    // ...
    DivergenceShader = UMaterialInstanceDynamic::Create(DivergenceShaderBase, this);
    // ...
}

void AFluidSimPawn::FluidDivergence(UTextureRenderTarget2D* OutDivergence, UTexture* InVelocity)
{
    DivergenceShader->SetTextureParameterValue(FName(TEXT("Velocity")), InVelocity);
    UKismetRenderingLibrary::DrawMaterialToRenderTarget(this, OutDivergence, DivergenceShader);
}

Resolver la presión. Jacobi.

No hemos detallado en qué consiste el Jacobi para resolver la ecuación Poisson. En este caso vamos a hacer un copy&paste del método tal cuál.

El siguiente material implementa una iteración de Jacobi:

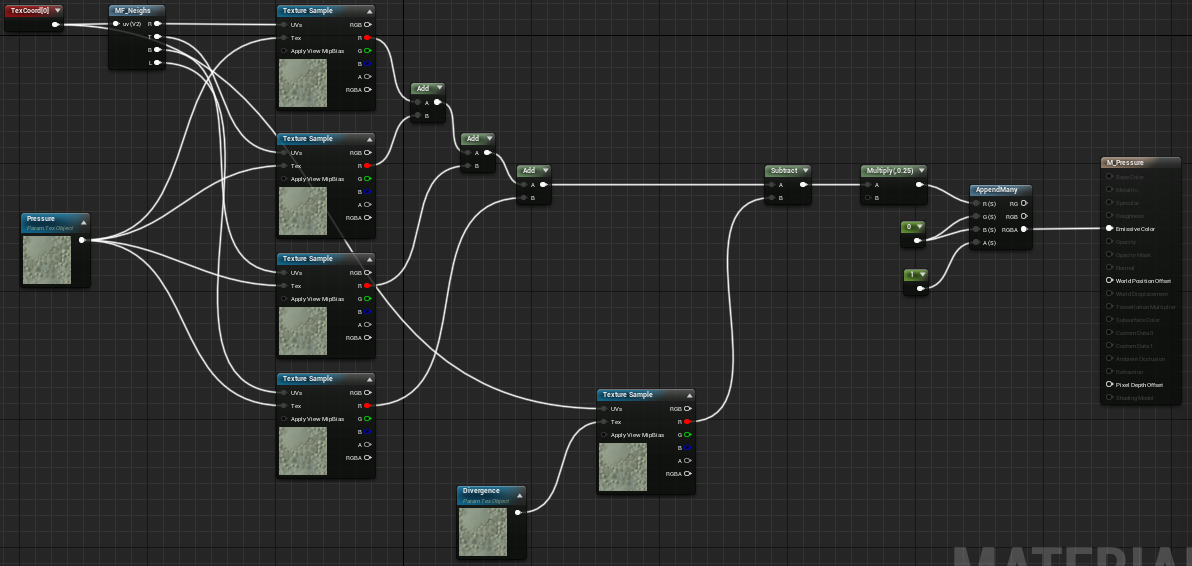
Ampliamos la clase FluidSimPawn:

public:
UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
UMaterialInterface* PressureShaderBase;

protected:
void FluidJacobiIteration(class UTextureRenderTarget2D* OutPressure, class UTexture* InPressure, class UTexture* InDivergence);

private:
UPROPERTY()
class UMaterialInstanceDynamic* PressureShader;

void AFluidSimPawn::BeginPlay()
{
    // ...
    PressureShader = UMaterialInstanceDynamic::Create(PressureShaderBase, this);
    // ...
}

void AFluidSimPawn::FluidJacobiIteration(class UTextureRenderTarget2D* OutPressure, class UTexture* InPressure, class UTexture* InDivergence)
{
    PressureShader->SetTextureParameterValue(FName(TEXT("Divergence")), InDivergence);
    PressureShader->SetTextureParameterValue(FName(TEXT("Pressure")), InPressure);
    UKismetRenderingLibrary::DrawMaterialToRenderTarget(this, OutPressure, PressureShader);
}

Gradiente. Corrección de la velocidad.

El último paso del algoritmo es corregir la velocidad usando el gradiente tal y como vimos en el apartado anterior sobre el algoritmo.

El siguiente material hace precisamente eso:

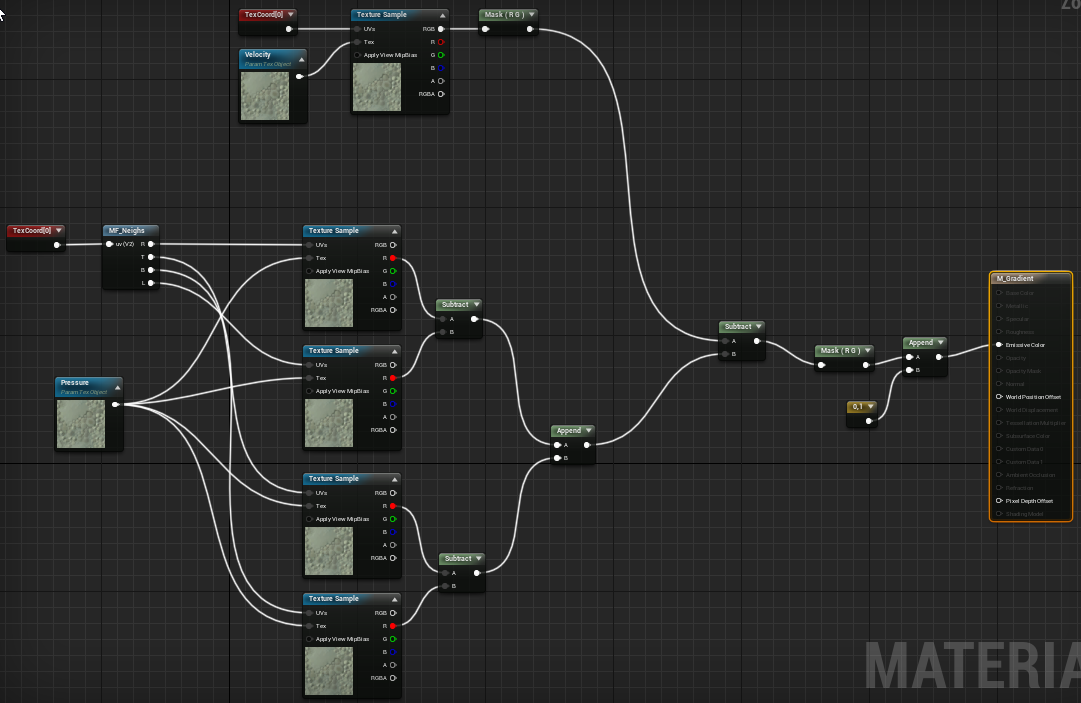
Ampliamos la clase FluidSimPawn:

public:
UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
UMaterialInterface* GradientShaderBase;

protected:
void FluidGradient(class UTextureRenderTarget2D* OutVelocity, class UTexture* InVelocity, class UTexture* InPressure);

private:
UPROPERTY()
class UMaterialInstanceDynamic* GradientShader;

void AFluidSimPawn::BeginPlay()
{
    // ...
    GradientShader = UMaterialInstanceDynamic::Create(GradientShaderBase, this);
    // ...
}

void AFluidSimPawn::FluidGradient(class UTextureRenderTarget2D* OutVelocity, class UTexture* InVelocity, class UTexture* InPressure)
{
    GradientShader->SetTextureParameterValue(FName(TEXT("Velocity")), InVelocity);
    GradientShader->SetTextureParameterValue(FName(TEXT("Pressure")), InPressure);
    UKismetRenderingLibrary::DrawMaterialToRenderTarget(this, OutVelocity, GradientShader);
}

Todo junto

Ya solo nos queda poner todas las piezas juntas.

Tal y como habíamos esbozamos cuando hablamos del algoritmo:

1. El primer paso será calcular el divergente del campo de la velocidad.
2. Posteriormente resolveremos el campo escalar presión usando jacobi.
3. Por último usaremos el gradiente para corregir la velocidad.

El algoritmo quedaría así:

void AFluidSimPawn::Tick(float DeltaTime)
{
    Super::Tick(DeltaTime);

    if (bIsPainting)
    {
        MovePaint();
    }	

    FluidStep(DeltaTime);
}

void AFluidSimPawn::FluidStep(float DeltaTime)
{
    FluidDivergence(DivergenceField, VelocityField);
    
    UKismetRenderingLibrary::ClearRenderTarget2D(this, PressureField);        
    for (int PresssureIter = 0; PresssureIter < NumberPressureIterations; ++PresssureIter)
    {
        FluidCopy(PressureFieldRead, PressureField);
        FluidJacobiIteration(PressureField, PressureFieldRead, DivergenceField);
    }    
    
    FluidCopy(VelocityFieldRead, VelocityField);
    FluidGradient(VelocityField, VelocityFieldRead, PressureField);    
}

Dónde NumberPressureIterations es un entero que puedes tener como atributo de la clase. Valores entre 40 y 60 funcionan bien.

Ahora nos queda actualizar el campo velocidad así como el colorante.

Advect

Tenemos una textura con la velocidad calculada y otra con el colorante.

¿Cuál es el color del colorante en el punto $P = (P_x, P_y)$ transcurrido un delta time ($dt$)?

Si $u = (u_x, u_y)$ es el vector velocidad en ese punto, entonces podemos deducir que el color del colorante en el punto $P$ es el color del colorante que ha arrastrado "la corriente", es decir, la cantidad de colorante en $P$ será la cantidad de colorante que había en un punto

$$ Q = P - u  dt = (P_x - u_x dt, P_y - u_y dt) $$

hace $-dt$ tiempo.

Lo mismo podemos decir de la propieda velocidad. En un fluido la velocidad "se arrastra" a si misma. Este término $ -(u \cdot \nabla) u $ en la ecuación de Naive-Stoke lo afirma. Este término suele tener el nombre de advect.

Vamos a implementar la simulación de la velocidad:

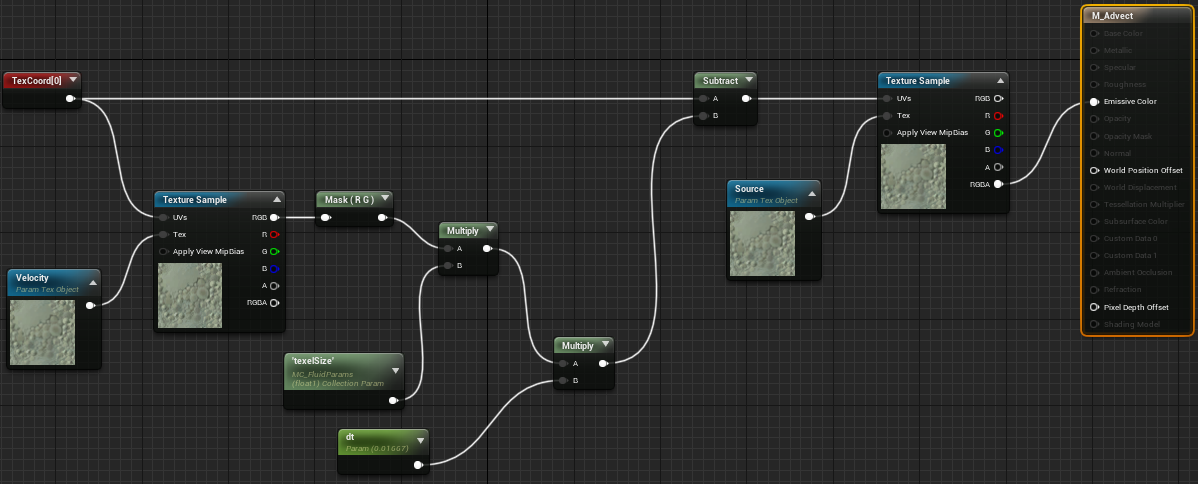
Y procedemos del mismo modo que con materiales anteriores:

public:
UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = "FluidSim")
UMaterialInterface* AdvectShaderBase;

protected:
void FluidAdvect(class UTextureRenderTarget2D* Advected, class UTexture* InSource, class UTexture* InVelocity, float DeltaTime);

private:
UPROPERTY()
class UMaterialInstanceDynamic* AdvectShader;

void AFluidSimPawn::BeginPlay()
{
    // ...
    AdvectShader = UMaterialInstanceDynamic::Create(AdvectShaderBase, this);
    // ...
}

void AFluidSimPawn::FluidAdvect(UTextureRenderTarget2D* Advected, UTexture* InSource, UTexture* InVelocity, float DeltaTime)
{	
    AdvectShader->SetTextureParameterValue(FName(TEXT("Velocity")), InVelocity);
    AdvectShader->SetTextureParameterValue(FName(TEXT("Source")), InSource);
    AdvectShader->SetScalarParameterValue(FName(TEXT("dt")), DeltaTime);
    UKismetRenderingLibrary::DrawMaterialToRenderTarget(this, Advected, AdvectShader);
}

Por último, actualiza la función FluidStep:

void AFluidSimPawn::FluidStep(float DeltaTime)
{
    // ...
    
    FluidCopy(VelocityFieldRead, VelocityField);
    FluidAdvect(VelocityField, VelocityFieldRead, VelocityFieldRead, DeltaTime);

    FluidCopy(DyeFieldRead, DyeField);
    FluidAdvect(DyeField, DyeFieldRead, VelocityField, DeltaTime);
}

Y ya tenemos la gloriosa simulación:

Proyecto completo

Puedes descargar el proyecto completo desde aquí. (Exclusivo para miembros).

Referencias

aadebdeb/WebGL_StableFluids

Stable Fluids in WebGL. Contribute to aadebdeb/WebGL_StableFluids development by creating an account on GitHub.

GitHubaadebdeb

Fluid Simulation for Video Games (part 1)

Simulation of fluids in games has been limited due to the computational challenges. This series of articles explains fluid dynamics and its simulation techniques.

IntelDr. Michael J. Gourlay

http://developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

https://www.mathematik.uni-dortmund.de/~kuzmin/cfdintro/lecture4.pdf